1、什么是卷积
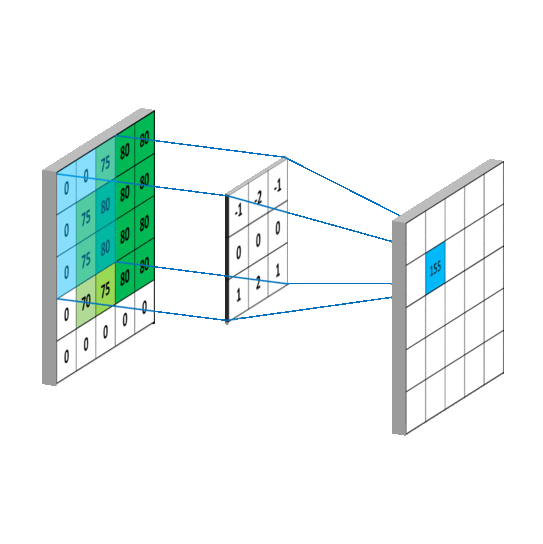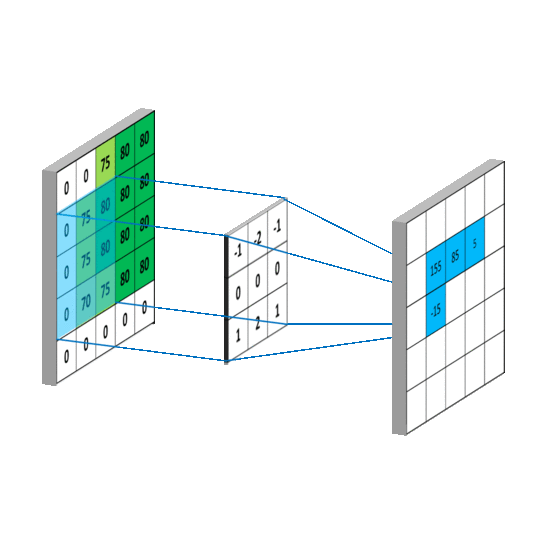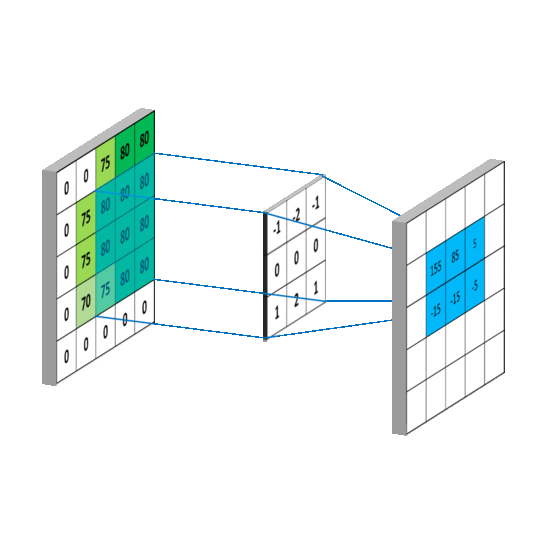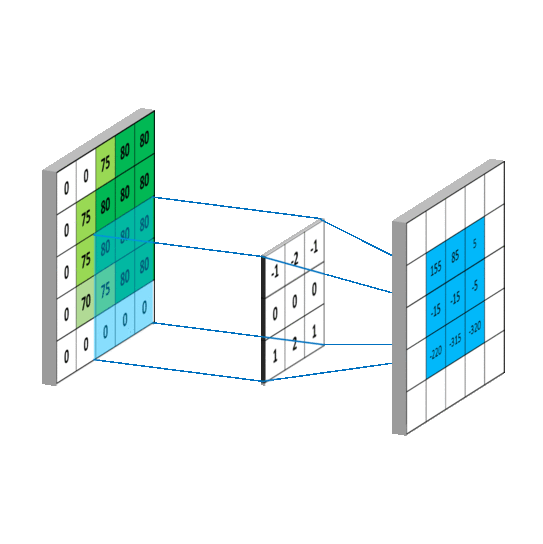
数字图像是一个二维的离散信号,对数字图像做卷积操作其实就是利用卷积核(卷积模板)在图像上滑动,将图像点上的像素灰度值与对应的卷积核上的数值相乘,然后将所有相乘后的值相加作为卷积核中间像素对应的图像上像素的灰度值,并最终滑动完所有图像的过程。
简言之,图像中不同数据窗口的数据和卷积核(一个滤波矩阵)作内积的操作叫做卷积,其计算过程又称为滤波(filter)。
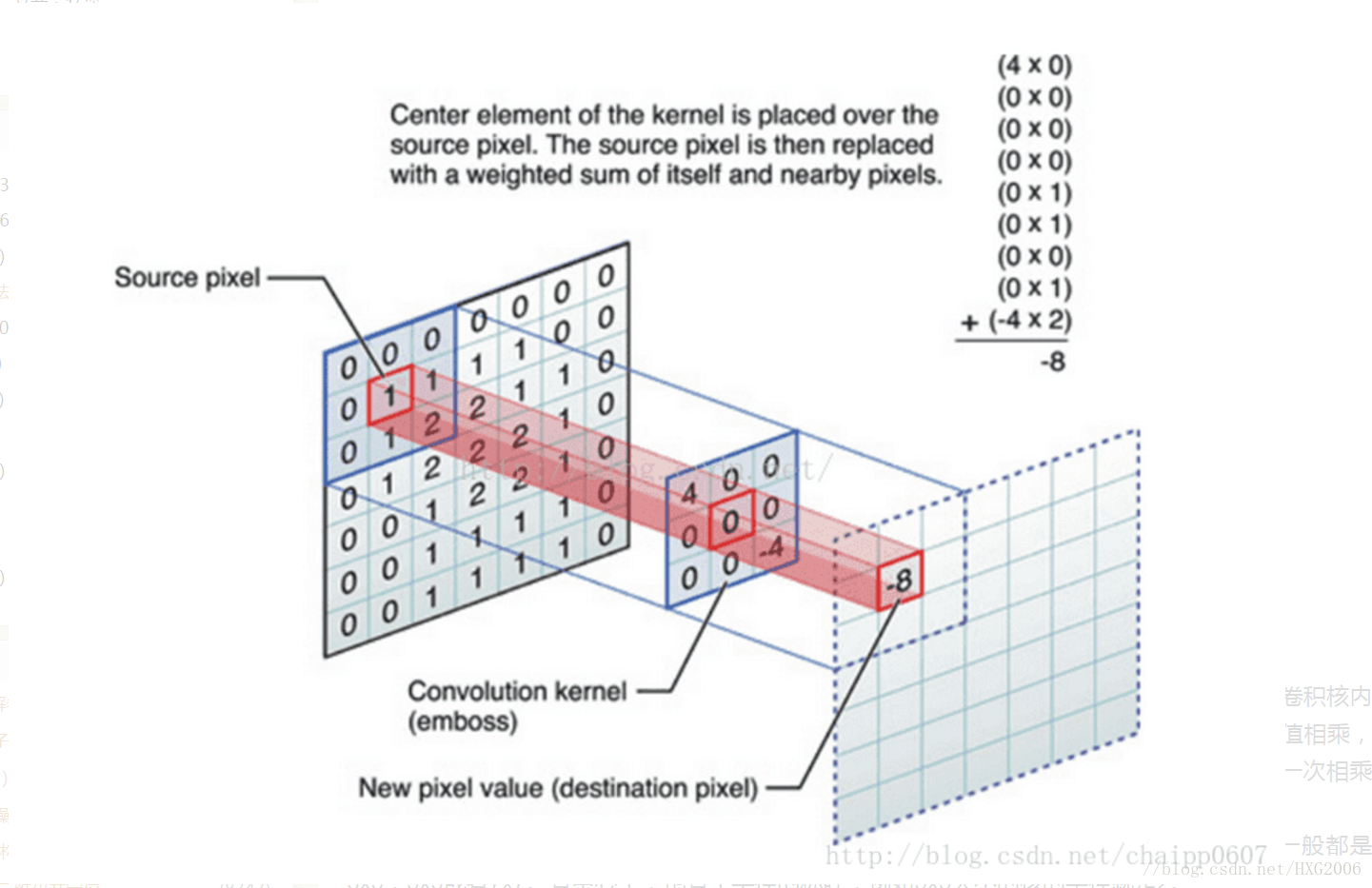
这张图可以清晰的表征出整个卷积过程中一次相乘后相加的结果:该图片选用3*3的卷积核,卷积核内共有九个数值,所以图片右上角公式中一共有九行,而每一行都是图像像素值与卷积核上数值相乘,最终结果-8代替了原图像中对应位置处的1。这样沿着图片一步长为1滑动,每一个滑动后都一次相乘再相加的工作,我们就可以得到最终的输出结果。
采取 2D 矩阵权重,把像素在水平和垂直方向上结合起来,在水平和垂直方向上保持空间布局。同样,记住已经有了水平和垂直方向的权重运动,输出会在水平和垂直方向上低一个像素。这个方法的另一个重大好处是它可以减少图像的参数数量。正如所见,卷积图像相比于原始图像有更少的像素。简言之,通过卷积操作,即压缩减少了图像的像素,而且还保留了相对的空间位置信息。
2、什么是卷积核:也称为滤波器filter,带着一组固定权重的神经元,通常是n*m二维的矩阵,n和m也是神经元的感受野。n*m 矩阵中存的是对感受野中数据处理的系数。一个卷积核的滤波可以用来提取特定的特征(例如可以提取物体轮廓、颜色深浅等)。通过卷积层从原始数据中提取出新的特征的过程又成为feature map(特征映射)。
在卷积神经网络中,有一个非常重要的特性:权值共享。
所谓的权值共享就是说,给一张输入图片,用一个filter去扫这张图,filter里面的数就叫权重,这张图每个位置是被同样的filter扫的,所以权重是一样的,也就是共享。
除此之外,卷积核的选择有一些规则:
1)卷积核的大小一般是奇数,这样的话它是按照中间的像素点中心对称的,所以卷积核一般都是3x3,5x5或者7x7。有中心了,也有了半径的称呼,例如5x5大小的核的半径就是2。
2)卷积核所有的元素之和一般要等于1,这是为了原始图像的能量(亮度)守恒。其实也有卷积核元素相加不为1的情况,下面就会说到。
3)如果滤波器矩阵所有元素之和大于1,那么滤波后的图像就会比原图像更亮,反之,如果小于1,那么得到的图像就会变暗。如果和为0,图像不会变黑,但也会非常暗。
4)对于滤波后的结构,可能会出现负数或者大于255的数值。对这种情况,我们将他们直接截断到0和255之间即可。对于负数,也可以取绝对值。
3、什么是卷积层:多个滤波器叠加便成了卷积层。
4、边界补充问题
上面的图片说明了图像的卷积操作,但是也反映出一个问题,如上面的动画图,原始图片尺寸为5*5,卷积核的大小为3*3,当卷积核沿着图片滑动后只能滑动出一个3*3的图片出来,这就造成了卷积后的图片和卷积前的图片尺寸不一致,这显然不是我们想要的结果,所以为了避免这种情况,需要先对原始图片做边界填充处理。在上面的情况中,我们需要先把原始图像填充为7*7的尺寸。
常用的区域填充方法包括:补零、边界复制、镜像、块复制,这些填充方法本文不再多做解释,详情见参考文献:卷积及理解图像卷积操作的意义。
5、不同卷积核下卷积的意义
我们经常能看到:平滑、模糊、去燥、锐化、边缘提取等等工作,其实都可以通过卷积操作来完成,下面我们举例说明一下:
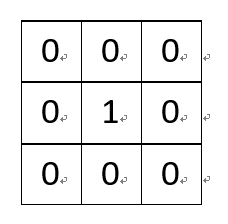
(1)一个没有任何作用的卷积核:
将原像素中间像素值乘1,其余全部乘0,显然像素值不会发生任何变化。
(2)平滑均值滤波,选择卷积核如下:
该卷积核的作用在于取九个值的平均值代替中间像素值,所以起到的平滑的效果:
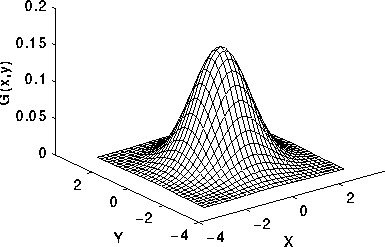
(3)高斯平滑,卷积核如下:
高斯平滑其水平和垂直方向呈现高斯分布,更突出了中心点在像素平滑后的权重,相比于均值滤波而言,有着更好的平滑效果。
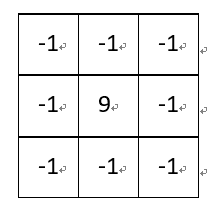
(4)图像锐化,卷积核如下:
该卷积利用的其实是图像中的边缘信息有着比周围像素更高的对比度,而经过卷积之后进一步增强了这种对比度,从而使图像显得棱角分明、画面清晰,起到锐化图像的效果。
(5)梯度Prewitt卷积核(6)Soble边缘检测卷积核(7)梯度Laplacian卷积核,在此不再详述,道理相通,详细内容可参阅:数字图像处理: 图像平滑 (均值滤波、中值滤波和高斯滤波)。
来源:
https://blog.csdn.net/hxg2006/article/details/79626288
https://blog.csdn.net/cheneykl/article/details/79740810
https://blog.csdn.net/zaishuiyifangxym/article/details/89788020
https://www.cnblogs.com/henuliulei/p/10559954.html
深入学习卷积神经网络(CNN)的原理知识
https://www.cnblogs.com/wj-1314/p/9754072.html